| Discrete Dynamics Lab |
Update
ddlabx11
New options for NULL boundary conditions |

NULL Basin of attraction field, ECA rule 150, n=11 |
DDLab has been updated at regular intervals since its release in 1995.
Its precursor was the Atlas software included on diskette
inside the back cover of "The Global Dynamics of Cellular Automata". For a list and download of this and older versions click here. Below are links to descriptions of previous updates, June 2012 Nov 2005 Dec 2003 July 2001 Feb 1999 Sept 1997 |
download
ddlabx11 for Linux, Mac, Cygwin and DOS
The new 2d hex/triangular neighborhoods for k3 and k4 permit investigating
the dynamics on these simpler lattices, with many instances of
complexity. This example: a 2d 122x122 triangular/hex lattice v3k4
rule 2a945900 from a random initial state --
black structures and glider-guns emerge.
More about this later ...
DDLab has been extended for Null Boundary
Conditions (NBC), where inputs beyond the network's edges are held at a
constant value of zero (though another value is possible). This
contrasts with Periodic Boundary Conditions (PBC), up till now the
only method adopted for cellular automata (CA) in DDLab.
NBC are of interest in pattern recognition, and other applications
where the system is grounded or quenched, or bounded by edge, skin or
membrane. As for PBC, NBC are also interesting as mathematical/dynamical systems
in their own right.
All DDLab functions and options for computation, display and analysis, as described
in the book "Exploring Discrete Dynamics" (EDD), can now also be
applied to NBC systems, multi-value as well as binary. This includes
CA in various dimensions, but also random Boolian networks (RBN) and
discrete dynamical networks (DDN), because irrespective of the wiring
scheme, for NBC any part of the pseudo-neighborhood that extends beyond the
network's edges is made to take zero as its input.
NBC space-time patterns (running forward) apply to 1d, 2d and 3d
networks -- toggling between NBC and PBC on-the-fly. All (forward)
functions and methods apply -- such as the look-up entropy, filtering,
damage, and attractor histograms.
NBC basins of attraction (running backward) apply to 1d networks by
means three completely different reverse algorithms, where the
original PBC algorithms have been modified for NBC: (1) for CA, (2)
for RBN/DDN as well as CA, and (3) the exhaustive reverse algorithm
for any of the above, thus providing a reality check of results. All
(backward) methods and functions for basin of attraction fields,
single basins and subtrees apply.
The new NBC functionality in DDLab opens up a new area of
phenomenology (as before for PBC) for quick and easy
investigation. Early results show that NBC basins of attraction are
very different from PBC. There is a greater chance of point attractors
or short periods. For CA with symmetric (odd size) neighborhoods
(k=3,5,7,...) the reflection transformation gives equivalent
dynamics/basins. Space-time patterns (including gliders) exhibit the
same dynamics away from edges, of course, but mobile structures are
usually quenched at the edges (resulting in shorter cycles and
taransients), or may sometimes interact (bounce) with the edges.
How to set Null Boundary Conditions in
ddlabx11
running forward:
At the prompt in EDD#31.1 there is an extra option:
boundaries-b.
If 'b' is entered, there is a further prompt (initially):
PERIODIC boundaries, set NULL-N:
or
NULL boundaries, set PERIODIC-P:
A change (to NULL) will be conserved unless backtracking to
the seed prompt, EDD#21.1.
running backward:
At the prompt in EDD#24.1 there is an extra option attached to the
existing "display" category, so now it reads ...
display/boundary-p
Attractor basins can be generated using three alternative reverse
algorithms selected in EDD#29.4. An acronym for the algorithm used now
appears in the top-right corner of the "attractor basin complete data
window" EDD#27.2, as follows ...
CAW ...CA wiring algorithm, the 1d direct algorithm, which allows mixed rules.
The following acronyms are also added, but do not relate to NULL boundaries.
Confirming previous NBC results for CA in the literature:
Rule 150, n=7 and n=11, fig. 1 [1].
NBC references
1. N.Pitsianis, Ph.Tsalides, G.L.Bleris, A.Thanailiakis, H.C.Card
"Deterministic One-Dimensional Cellular Automata"
Journal of Statistical Phisics, Vol.36. Nos.1/2, 1989.
2. John G. Stevens, ~ Ronald E. Rosensweig, 2 and A. E. Cerkanowicz,
"Transient and Cyclic Behavior of Cellular Automata with Null Boundary Conditions"
Journal of Statistical Physics, Vol 73, No.1/1, 1993.
3. Sudhakar Sahoo, Pabitra Pal Choudhury
"Issues on drawing the State Transition Diagram for arbitrary Cellular Automata",
Applied Statistics Unit, Indian Statistical Institute, Kolkata, 700108, INDIA,
(where published? 2008).
4. Sukanta Das, DPhil, 2006
"Theory and Applications of Nonlinear Cellular Automata In VLSI Design",
Department of Computer Science and Technology, Bengal Engineering And Science University
5. Nazma Naskari, Sukanta Das, Biplab Sikdar
"Characterization of nonlinear cellular automata having only single length cycle attractors"
JCA, 2012 (to appear).
summary of updates
(EDD#x.x.x refers to the relevant chapter or
section in "Exploring Discrete Dynamics")
click to enlarge
New 2d hex/triangular neighborhoods for k3 ![]() and k4
and k4 ![]()
Return to the
Discrete Dynamics Lab home page.
examples -- click to enlarge 
ECA rule 225 n=14 - Periodic boundaries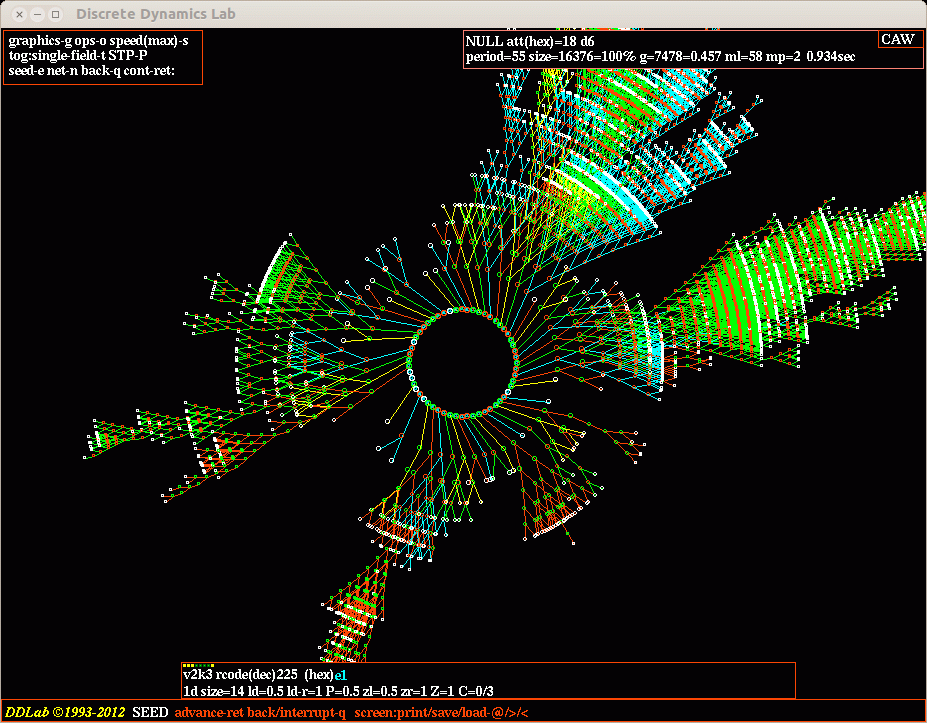
ECA rule 225 n=14 - Null boundaries
ECA rule 110 n=4 to 11 - Null boundaries
ECA rule 110 space-time patterns n=150
Null boundaries.
Cells colored by neighborhood lookup EDD#32.9.5
ECA rule 52 n=4 - Null boundaries [3]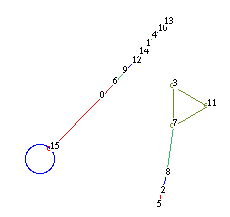
mixed ECA rules 105,177,171,75 - Null boundaries [4]
mixed ECA rules 5,73,200,80 - Null boundaries [5]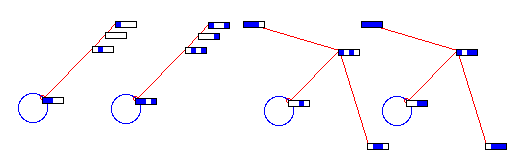
mixed ECA rules 10,69,204,68 - Null boundaries [5]
Null Boundary Condition
for Cellular Automata and Discrete Dynamical Networks
While space-time patters are running, PERIODIC/NULL can be toggled
on-the-fly with key hit '|' (vertical bar symbol).
The current status appears in the "on-the-fly key index" EDD#32.1,
either "Periodic/NULL" or "NULL/Periodic"
If 'p' is entered, the next prompt EDD#26.1 shows the current
setting, PERIODIC initially, and an option to change to NULL ...
PERIODIC boundaries (compression ON, off-s:) NULL-N:
or vice-vera ...
NULL boundaries (compression OFF) PERIODIC-P:
A change (to NULL) will be conserved unless backtracking to the seed
prompt, EDD#21.1 (for single basins and subtrees) or (for a basin of
attraction field) to the neighbourhood size prompt EDD#9.1.
PERIODIC or NULL appears in the
top-left corner of the "attractor basin complete data window"
EDD#27.2.
NLW ...non-local wiring algorithm, for CA, RBN, DDN, which allows mixed k.
EXH ...exhaustive algorithm #29.7, for CA, RBN, DDN (required for MAP, and sequential updating).
MAP ...random map #29.8, using the EXH algorithm (PERIODIC/NULL is irrelevant).
SEQ ...sequential updating #29.9, using the EXH algorithm (disabled for NULL).
NTO ...neutral order components #29.10, related just to wiring (disabled for NULL).
Rule 90, n=1 to 40, Table 1. Transient and Cycle Lengths [2]
(checked by attractor basins and attractor histogram).
Rule 52, n=5, fig.1 [3].
Mixed rule CA 105,177,171,75, n=4, Fig.3.5 [4].
Mixed rule CA 5,73,200,80, n=4, Fig.1 [5].
Mixed rule CA 10,69,204,68, n=4, Fig.5 [5].
Last modified: Jan 2013